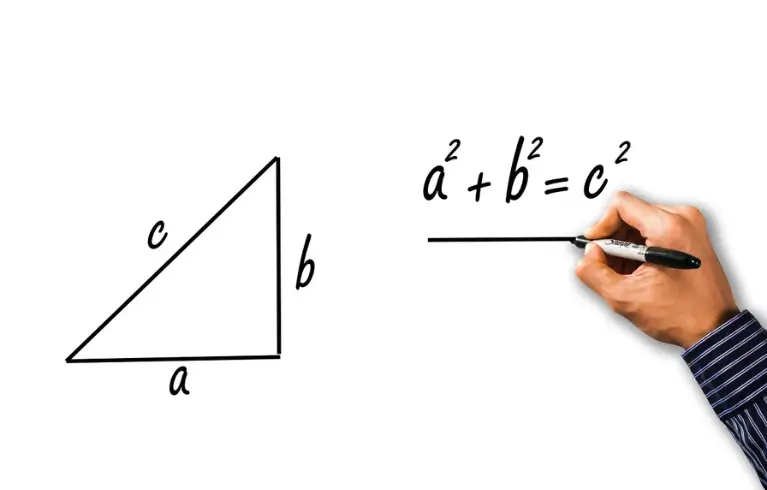Embarking on the journey of Class 10 Maths is an essential step in every student’s academic path. With our meticulously designed NCERT Solutions, students can navigate through each chapter with confidence and clarity. From Real Numbers to Probability, our solutions encompass a comprehensive range of topics to ensure a thorough understanding of mathematics. In the … Read more
Embarking on the journey of Class 9 Maths can be both exciting and challenging. However, with our meticulously crafted NCERT Solutions, mastering each chapter becomes a breeze. From Number Systems to Probability, our website offers comprehensive guidance to ensure a strong foundation in mathematics. Chapters of Class 9 Maths Chapter 1: Number Systems Understanding number … Read more
Are you a student struggling to grasp the concepts of Class 8 Maths? Look no further! Our website provides optimized NCERT Solutions tailored to help you conquer every chapter, from Rational Numbers to Playing with Numbers. Whether you’re facing challenges in Linear Equations or seeking clarity in Data Handling, our meticulously crafted solutions ensure a … Read more
Looking for Class 7 Maths NCERT solutions? Look no further! Our website offers comprehensive resources to help you understand and excel in this subject. Join us now! Are you struggling with understanding the concepts of Class 7 Maths? Look no further! Our detailed NCERT solutions for each chapter are here to guide you through every … Read more
Need help with Class 6 Maths? Look no further! Find comprehensive NCERT Solutions to boost your understanding and grades. Mathematics is often regarded as the language of the universe, providing a systematic way to understand and interpret the world around us. For students embarking on their mathematical journey, NCERT Solutions serve as invaluable companions, offering … Read more
The Class 5 Maths NCERT Solutions talks about lots of things like numbers, shapes, measuring, and more. They are made to help fifth graders learn better and understand tricky math stuff. By using these solutions, students can get better at math and really understand how it all works. NCERT Solutions If you’re having trouble with … Read more
Imaginary numbers, also known as complex numbers, are a fundamental concept in mathematics. They are defined as numbers that involve the imaginary unit, denoted by the symbol “$i$,” which is defined as the square root of $-1$. The Imaginary number is often represented in the form $a + bi$, where “$a$” and “$b$” are real … Read more
Algebraic equations are mathematical expressions that involve variables and constants. When solving algebraic equations, the goal is to find the value of the variable that makes the equation true. This process often involves isolating the variable on one side of the equation by performing various operations such as addition, subtraction, multiplication, and division. Types of … Read more
Welcome to the fascinating world of mathematics, where we delve into the concept of rational exponents. We explore the importance of this topic in bridging the gap between integer exponents and radicals. In this article, we will explore fractional exponents in-depth, shedding light on their significance and practical applications. What Are Rational Exponents? Rational exponents, … Read more
Within the domain of algebra, the ability to perform polynomial division is a fundamental skill that holds considerable importance in the simplification of intricate expressions, the factorization of polynomials, and the resolution of equations. Among the diverse techniques available for polynomial division, the long division of polynomials is particularly noteworthy for its methodical approach to … Read more
Step into the fascinating world of mathematics and discover the hidden gems that lie within rational numbers. These little wonders are the building blocks of all mathematical concepts, from the basic to the advanced. They are the key to unlocking the mysteries of numerical understanding and unleashing the full potential of mathematical applications. We will … Read more
Calculus 1, the mathematical wizardry behind change and motion, holds immense power in unraveling the secrets of our world. Whether you’re a high school student embarking on a mathematical adventure or a university student delving deeper into its mysteries, this article will be your guide to the captivating realm of calculus. Foundations of Calculus 1: … Read more